"The Holy Grail" of Cryptography
The rapid advancement of technology over recent decades has led to a growing popularity of cryptography. Terms that were once known only to mathematician-cryptographers have become widely recognized, including "Homomorphic Encryption".
Let us try to understand what problems standard encryption algorithms solve, what their limitations are, and why homomorphic encryption was needed.
Classical cryptographic schemes perform some parametric (key-dependent) mapping of the public data space into the encrypted data space. At the same time, it is possible to invert this transformation only by having this very parameter (key)
A characteristic feature of encryption algorithms is the scattering and mixing of information representing the plaintext. As a consequence, the metrics defined in the plaintext space are not preserved.
For example, the results of encrypting two input plaintexts on the same key, which differ only in one bit, are not close to each other in the ciphertext space. In turn, any change in the data representing the ciphertext leads to the fact that, decrypting it, we will get just random uninterpreted data.
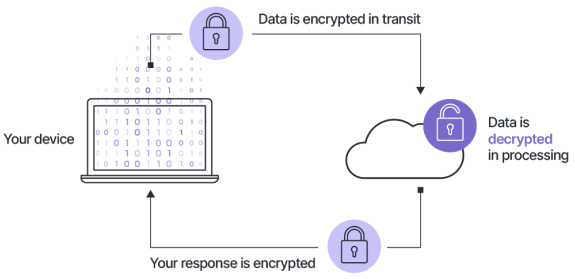
It can be stated that the era of 'big data' has already arrived. The development of machine learning has changed many areas of life, including the emergence of cloud computing platforms that provide users with significant computing power and various services for data processing.
Customers can protect their data while transferring it to the cloud, but to perform data processing and analysis, the data must be decrypted
Thus, the client provides his data, possibly entrusted to him by third parties, to a resource beyond his control, which multiplies the probability of leakage or unauthorized access.
There are various approaches to solve this problem, for example, physical isolation of servers, limiting the interaction of third parties with it. However, in any of these cases, the client is forced to believe, in fact, on bare word and entrust his data to the protection implemented on the server side.
Naturally, there is a desire to provide its data with its own protection, as in the case of transmission, when it is not necessary to rely only on the implementation of transport protocol protection, you can send already encrypted data.

The concept of an encryption scheme allowing operations on encrypted data in such a way that the decryption of the result is a correct transformation of the public data corresponding to the operated ciphertexts, has been floating in the cryptographic environment for about 30 years and is often called the “Holy Grail” of cryptography.
However, this idea was rather difficult to achieve.
The initial efforts towards developing encryption schemes that allow certain operations on encrypted data coincide with the work on public-key encryption schemes, which were originally designed for different purposes.
Large prime numbers p and q are chosen, and N = pq – is computed as the system's modulus, φ(N) = (p-1)(q-1) – the Euler's totient function, eЄZ*N is selected and the corresponding d is determined such that ⅇ ⋅d ≡ 1(mod ϕ(N)). The public key of the system is formed as (e, N), and the private key is (φ(N),d).
The encryption algorithm for a message m is given by Enc(x)=me (mod N), with the result denoted as с. The decryption algorithm is Dec(c) = сd(mod N).
The correctness is ensured by the fact that cd (mod N) = (ce)d (mod N) = m(mod N), because ⅇ⋅d ≡ 1(mod φ(N)).
In the given scheme, the space of plaintexts coincides with the space of ciphertexts and is represented by ZN. Suppose we have two ciphertexts с1 and с2, corresponding to messages m1 and m2 respectively. Consider the product с1 ⋅ с2(mod N) and let's attempt to decrypt it.
Dec(с1 ⋅ с2) = (с1 ⋅ с2)d (mod N) = (m1e ⋅ m2e)d(mod N) = (m1 ⋅ m2)ed (mod N) = m1 ⋅ m2(mod N).
From this, we can see that the product of two ciphertexts is a valid ciphertext for the product of the corresponding plaintexts. Such mappings are called homomorphic with respect to the operations for which these properties hold. Specifically, the functions Enc() and Dec() are multiplicatively homomorphic.
Multiplicative homomorphism is not sufficient for most data processing tasks. Because of this, the search for cryptographically robust algorithms with encryption/decryption functions that are homomorphic with respect to a larger number of operations is the main challenge for the development of this area.
Classical machine learning and deep learning can be decomposed into a set of fundamental operations on data or approximated by a series of basic operations. Thus, using secure ML algorithms on encrypted data is equivalent to applying the original versions of these algorithms to unencrypted data. In this scenario, data can be analyzed while remaining encrypted.
For example, consider a messaging system where messages need to be encrypted end-to-end, from sender to receiver. At the same time, it is necessary to check these messages for spam without compromising their confidentiality.
In this way, homomorphic encryption restores control over data to its owners.
However, it is important to understand that it is not a cryptographic panacea and cannot replace more high-performance schemes. Nevertheless, similar to public-key cryptosystems, it can carve out its own niche.